Un diagrama de caja, también conocido como diagrama de bigotes, es una representación visual que muestra la distribución de un conjunto de datos junto con varias medidas estadísticas clave. Proporciona un resumen gráfico de información importante sobre un conjunto de datos, incluida la puntuación mínima, el primer cuartil, la mediana, el tercer cuartil y los valores máximos.
El diagrama de caja parece un rectángulo, a menudo llamado caja, que indica el rango intercuartil. El centro del cuadro representa la mediana y los lados exteriores del cuadro representan el primer cuartil (percentil 25) y el tercer cuartil (percentil 75), respectivamente. Los “bigotes” que se extienden desde el cuadro muestran el rango de datos, excluyendo los valores atípicos.
El diagrama de caja fue introducido por primera vez por el matemático John Tukey en 1970.
Este artículo analiza lo que un diagrama de caja puede decirle sobre un conjunto de datos y las diferentes partes de un diagrama de caja. También cubre cómo los diagramas de caja pueden ayudarlo a analizar datos y cómo interpretarlos.
¿Qué información le brindan los diagramas de caja?
Un diagrama de caja proporciona una serie de puntos clave de datos que pueden ayudar a revelar detalles e información importantes sobre los datos que describen.
Algunos de estos puntos clave incluyen la mediana, el rango intercuartílico y los valores mínimo y máximo excluyendo los valores atípicos.
Los 7 elementos de un diagrama de caja
Los siete elementos clave de un diagrama de caja son:
Puntuación mínima
La puntuación mínima es el punto de datos más bajo que excluye cualquier valor atípico.
Mediana
La línea dentro del cuadro indica la mediana de un conjunto de datos. La mediana es el valor medio del conjunto de datos cuando los valores están alineados en orden. Este número es importante porque indica la tendencia central del conjunto de datos.
Percentil inferior
También conocido como primer cuartil o percentil 25, es la mediana de la mitad inferior del conjunto de datos.
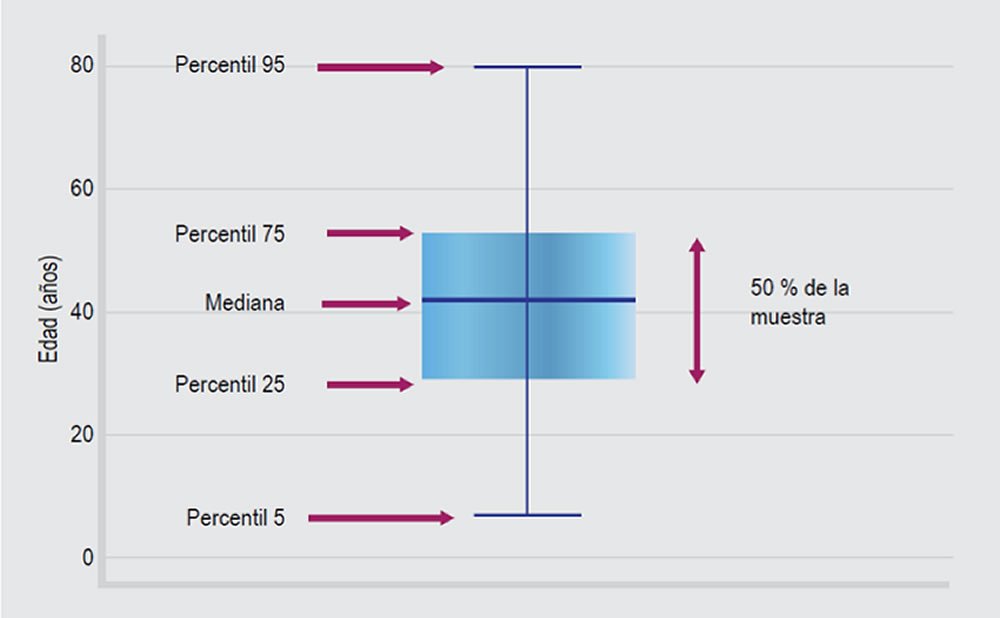
Percentil superior
También conocido como tercer cuartil o percentil 75, es la mediana de la mitad superior del conjunto de datos.
Puntuación máxima
Este es el punto de datos más alto del conjunto de datos una vez que se han excluido los valores atípicos.
Bigotes
Los “bigotes” del diagrama de caja son las líneas que se extienden desde ambos lados de la caja. Estas líneas representan el rango de datos sin los valores atípicos. Esto puede resultar útil para obtener información sobre los valores mínimos y máximos dentro de un rango determinado.
El rango intercuartil (IQR)
El cuadro en un diagrama de caja representa el rango intercuartil del conjunto de datos. El IQR es el rango entre el primer cuartil y el tercer cuartil. Contiene el 50% central de los datos y es útil para visualizar la distribución del conjunto de datos.
Los diagramas de caja no son paramétricos, lo que significa que no hacen suposiciones sobre la distribución subyacente de los datos. En cambio, funcionan para brindar una representación visual basada en la mediana y los cuartiles.
Esto los hace útiles para comparar datos entre diferentes grupos o condiciones. Proporcionan un resumen conciso de las principales características de los datos al transmitir rápidamente la tendencia central y la dispersión.
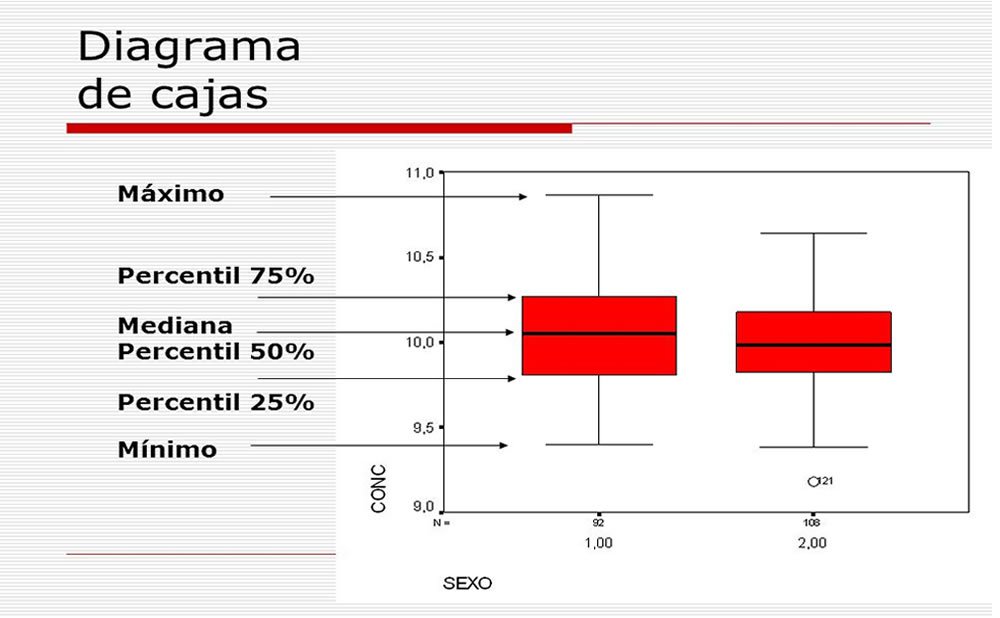
Orientación del diagrama de caja
Los diagramas de caja se pueden presentar horizontal y verticalmente. A menudo se presentan verticalmente en artículos académicos profesionales.
¿Por qué son útiles los diagramas de caja para analizar datos?
Los diagramas de caja tienen varios usos y beneficios importantes a la hora de transmitir y analizar datos en la investigación en psicología.
Estas representaciones gráficas pueden transmitir rápidamente información importante sobre la extensión y la simetría de una distribución. Con estas herramientas, es posible crear comparaciones visuales de diferentes grupos de datos.
Los investigadores también sugieren que los diagramas de caja pueden ayudar a las personas a mejorar su capacidad para interpretar y comprender información compleja. Esto permite a las personas razonar más eficazmente sobre información cuantitativa.
Los diagramas de caja también pueden ser una buena alternativa a los histogramas. Mientras que para un histograma generalmente se recomienda tener un tamaño de muestra mínimo de 50 puntos de datos, un diagrama de caja puede ser efectivo con un tamaño de muestra de solo cinco.4 Los diagramas de caja también se pueden adaptar de varias maneras para ayudar a mejorar la comparación y la interpretación. . Por ejemplo, se puede agregar una muesca al cuadro para mostrar el intervalo de confianza del 95% para la mediana.
Desde los sistemas principales hasta los procesos celulares, adquiere una comprensión profunda de cómo opera el cuerpo en su totalidad. Con lecciones interactivas y ejercicios prácticos, estarás preparado para aplicar estos conocimientos en el campo de la medicina, la biología y más.
Cómo interpretar un diagrama de caja
Al interpretar datos en un diagrama de caja, los investigadores suelen seguir una serie de pasos o métodos para obtener información y sacar conclusiones. Estos son los pasos comunes que se utilizan para interpretar los datos en un diagrama de caja:
Mire las características clave de los datos
El primer paso al interpretar un diagrama de caja es observar algunas de las características más importantes de los datos:
Identifique la mediana
La mediana está representada por la línea dentro del cuadro en el diagrama de caja. Divide los datos en dos mitades iguales, con el 50% de los datos por debajo y el 50% por encima de la mediana. Proporciona una medida de tendencia central.
Determine los cuartiles
El cuadro en el diagrama de caja representa el rango intercuartil (IQR). El cuartil inferior (Q1) es la mediana de la mitad inferior de los datos y el cuartil superior (Q3) es la mediana de la mitad superior. El IQR es el rango entre Q1 y Q3 y contiene el 50% medio de los datos.
Considere el rango
El rango de los datos, indicado por la longitud de los bigotes, proporciona una comprensión de la dispersión de los datos. Una amplia gama estaría indicada por bigotes más largos. Los bigotes cortos, por otro lado, indicarían un rango estrecho. Un rango amplio sugiere una mayor variabilidad en los datos.
Busque signos de datos inusuales
También puede resultar útil buscar señales de que sus datos puedan estar sesgados o ser inusuales de alguna manera.
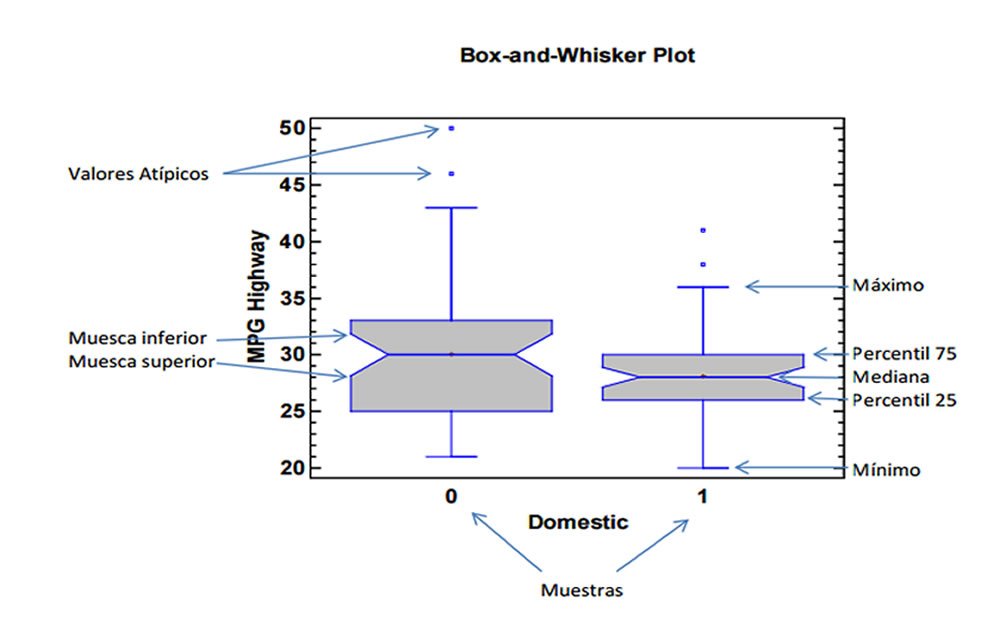
Identificar valores atípicos
Los valores atípicos son puntos de datos que se encuentran significativamente por encima o por debajo de los bigotes del diagrama de caja. Están indicados por puntos individuales o puntos fuera de los bigotes. Los valores atípicos pueden representar valores extremos o puntos de datos que se desvían significativamente de la mayoría.
Busque datos sesgados
Los datos muy sesgados pueden ser una señal de que no son normales. Puede evaluar la asimetría observando la ubicación del cuadro en la línea central y la ubicación de la mediana en relación con el cuadro. Si la mediana está más cerca de Q1, la distribución puede estar sesgada hacia la izquierda, mientras que, si está más cerca de Q3, la distribución puede estar sesgada hacia la derecha. Si sus datos parecen inusualmente sesgados, es importante investigar qué podría estar causándolos.
Analizar la simetría
La simetría del diagrama de caja puede indicar la simetría de la distribución de datos. Si el cuadro es aproximadamente simétrico, sugiere una distribución simétrica. Los cuadros asimétricos pueden sugerir asimetría u otras características de la distribución.
Hacer comparaciones
Los diagramas de caja se pueden utilizar para comparar distribuciones entre diferentes grupos o categorías. Los investigadores pueden identificar diferencias o similitudes en los datos comparando visualmente la posición, forma y extensión de las cajas y los bigotes.
Mire las muescas
Si está evaluando un diagrama de caja, las muescas en los lados de la caja pueden proporcionar una comparación visual de la incertidumbre entre grupos. Si las muescas no se superponen, las medianas pueden ser significativamente diferentes.
Mire las medianas
Si la línea mediana de un cuadro se encuentra fuera del cuadro del otro grupo, es una buena señal de diferencias entre los dos grupos.
Considere el tamaño de la muestra
Al comparar diagramas de caja, es importante considerar los tamaños de la muestra. Un tamaño de muestra pequeño puede no ser representativo de toda la población, por lo que las conclusiones deben sacarse con cautela.
Compare las longitudes de las cajas y los bigotes
Comparar las longitudes de las cajas (el rango intercuartil) y los bigotes (la distribución general de datos) también puede proporcionar información valiosa al comparar grupos. Las diferencias significativas en la longitud de las cajas y los bigotes sugieren diferencias entre los grupos.
Seguir estos pasos puede ayudarle a interpretar los datos que representan los diagramas de caja y obtener información a partir de las representaciones visuales de los datos.
Eso no significa que los diagramas de caja sean siempre la mejor opción para presentar datos. Pueden resultar útiles para comparar grupos, pero una representación visual más detallada, como un histograma, puede ser más informativa si se analiza un único conjunto de datos.
Cómo comparar diagramas de caja
Los diagramas de caja son una forma útil de visualizar diferencias entre diferentes muestras o grupos. Se las arreglan para proporcionar mucha información estadística, que incluye medianas, rangos y valores atípicos.
Tenga en cuenta que, aunque los diagramas de caja se presentaron horizontalmente en este artículo, es más común verlos verticalmente en los artículos de investigación.
Paso 1: comparar las medianas de los diagramas de caja
Compare las medianas respectivas de cada diagrama de caja. Si la línea mediana de un diagrama de caja se encuentra fuera del cuadro de un diagrama de caja de comparación, entonces es probable que haya una diferencia entre los dos grupos.
Paso 2: comparar los rangos intercuartiles y los bigotes de los diagramas de caja
Compare los rangos intercuartílicos (es decir, las longitudes de las cajas) para examinar cómo se dispersan los datos entre cada muestra. Cuanto más largo es el cuadro, más dispersos están los datos. Cuanto más pequeños, menos dispersos están los datos.
A continuación, observe la distribución general como lo muestran los valores extremos al final de dos bigotes. Esto muestra el rango de puntuaciones (otro tipo de dispersión). Los rangos más grandes indican una distribución más amplia, es decir, datos más dispersos.
Paso 3: busque posibles valores atípicos (consulte la imagen de arriba)
Al revisar un diagrama de caja, un valor atípico se define como un punto de datos que se encuentra fuera de los bigotes del diagrama de caja.
Paso 4: busque signos de asimetría
Si los datos no parecen ser simétricos, ¿muestra cada muestra el mismo tipo de asimetría?
¿Debería usar el diagrama de cajas o los gráficos de barra??
¿Qué tipo de datos representarás? ¿Cómo quieres representar tus datos? Debe responder estas preguntas antes de elegir entre las dos.
Algunos autores sostienen que no deberían utilizarse gráficos de barras, mientras que otros afirman que deberían surgir nuevos formatos para representar los datos. Los gráficos de barras agrupadas son útiles para mostrar los presupuestos de dos hogares, por ejemplo. Un uso común de los gráficos de barras es mostrar la proporción de un valor frente a otro.
Por otro lado, los diagramas de caja son útiles para trazar varios conjuntos de datos de fuentes independientes. Un ejemplo incluye puntuaciones de exámenes entre diferentes universidades, cambios en los datos (antes y después) debido a un proceso o datos de diferentes máquinas que fabrican el mismo producto. Los diagramas de caja son buenas formas de representar la distribución de sus datos, especialmente si su objetivo es mostrar otros valores además de la media.
Atar los datos de su investigación después de decidir que tipo de grafico usar
Es sencillo una vez que decide qué tipo de gráfico se adapta mejor a sus datos. Por ejemplo, si sus datos están sesgados, se puede utilizar un diagrama de caja. El lector podrá saber si los datos están sesgados hacia la izquierda o hacia la derecha, dependiendo de la longitud de la barra por encima y por debajo de la línea mediana. Los datos de ANOVA también se pueden mostrar mediante un diagrama de caja. Si sus datos son principalmente descriptivos y desea mostrar proporciones, entonces un gráfico de barras es su mejor opción.
Cualquiera que sea la forma que elija, es importante comprender la utilidad de estos gráficos. ¡El análisis de los datos de su investigación es la parte principal de su informe de investigación de manera efectiva! ¡Háganos saber lo que piensa sobre el uso de diagramas de cajas y gráficos de cajas al informar sus resultados!


